Parametrizing Curves in <math> \R^{3} </math>

We often think of a curve as an object drawn on paper, such as a straight line, curve, ellipse. A curve can be thought of as a more general object defined in space, defined mathematically as a function that maps an interval of real numbers into the space <math> \R^{3} </math>. Conventionally this map is denoted by <math> \vec r </math>, and the image of the interval corresponds to the curve C. We can write this as follows:

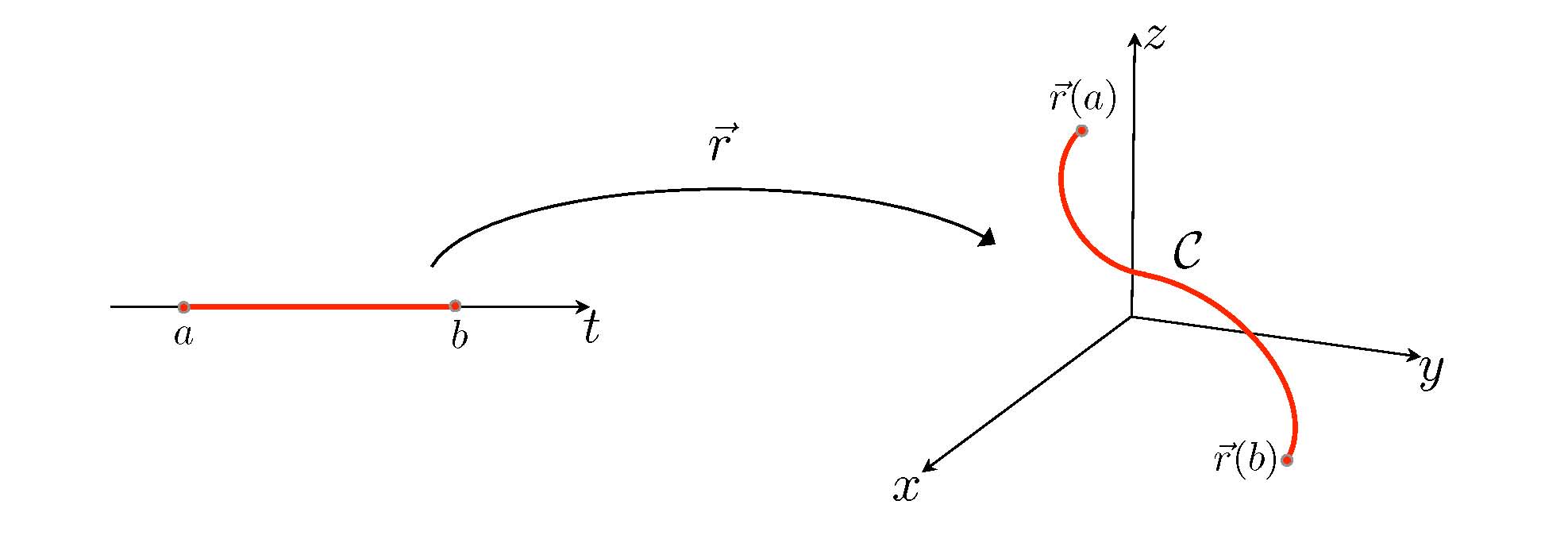
A curve in <math> \R^3 </math> is a map <math> \vec r: [a,b] \in \R \longrightarrow \R^{3} </math>. The collection C of points <math> \vec r(t) </math> as <math> t </math> varies in <math> [a,b] </math> is called a curve and <math> \vec r(a) </math> and <math> \vec r(b) </math> are its endpoints. In this way, the map <math> \vec r </math> is said to parametrize the curve C .

Expanded out in coordinates, we can write

<math> C: \vec r(t) = (x(t), y(t), z(t)), t \in [a,b] </math>.

Examples

You can play with any combination of functions <math>x(t), y(t), z(t) </math> to create curves in space, but it is useful to have a working knowledge of parametrizations of familiar curves. An important point to notice in these examples is that parametrizations are not unique, which will have consequences later when we want to access points along the curve.

First, let's start with some curves in the plane . (Technically, we could define a curve in the plane as being a map <math> \vec r: [a,b] \in \R \rightarrow \R^{2} </math> but here we simplify by just assuming that the last coordinate function <math> z(t) = 0 </math>)

Any graph in the plane given by <math> y = f(x) </math> in the interval <math> x \in [a,b] </math> can be parametrized by setting <math> x = t, y = f(t), z = 0 </math> so

<math> \vec r(t) = (t, f(t), 0), t \in [a,b] </math>

Notice that both <math> \vec r_1(t) = (t, t^2, 0), t \in [0,2] </math> and <math> \vec r_2(t) = (t, 4t^2, 0), t \in [0,1] </math> parametrize the same part of the parabola so there is nothing unique about parametrizations.

A circle in the plane centered at the origin with radius R can be parametrized as

<math> \vec r(t) = (R \cos{t}, R \sin{t}, 0) , t \in [0, 2 \pi] </math>

Note that we can recover the usual equation for the circle since <math> x(t)^2 + y(t)^2 = R^2 (\cos{t}^2 + \sin{t}^2 ) = R^2 </math>.

By limiting the interval, we can as easily define an arc , or a circular segment. In the parametrization above, <math> t </math> has the physical interpretation of the angle swept out counterclockwise, so the arc defined by <math> t \in [\pi/2, \pi] </math> is the segment in the second quadrant.

Similarly, an ellipse in the plane centered at the origin with semimajor axis A and semiminor axis B can be parametrized as

<math> \vec r(t) = (A \cos{t}, B \sin{t}, 0) , t \in [0, 2 \pi] </math>

Again, the usual equation for the ellipse can be recovered since <math> \frac{x(t)}{A}^2 + \frac{y(t)}{B}^2 = \cos{t}^2 + \sin{t}^2 = 1 </math>.

Let's move on to curves in space .

The most simple curve is the line , which in <math> \R^3 </math> is very conveniently described as

<math> \vec r(t) = \vec r_0 + t \vec v </math>

where <math> \vec r_0 </math> has its head as any point on the line and <math> \vec v </math> is a vector in the direction of the line.

Suppose <math> P_1 = (x_1, y_1, z_1) </math> and <math> P_2 = (x_2, y_2, z_2) </math> are two points on the line. Then the line segment between P_1 and P_2 is given by

<math> \vec r(t) = \vec p_1 + t(\vec p_2 - \vec p_1) = (x_1 + t (x_2 - x_1), y_1 + t (y_2 - y_1), z_1 + t (z_2 - z_1)), t \in [0, 1] </math>

The helix <math> \vec r(t) = (\cos{t},\sin{t}, t) </math> wraps around the cylinder resulting from extruding a circle of radius 1 in the vertical direction. Can you come up with parametrizations for a helix with a tighter or looser spiral?

A conical helix which spirals around the cone given by <math> z = \sqrt{x^2 + y^2} </math> can be parametrized as

<math> \vec r(t) = (t \cos{t}, t \sin{t}, t), t \in [0, T] </math>