| Week 3 | |
|---|---|
| Course | Arch 2042 |
| Date | 2012/03/09 |
| Learning Objectives | We will start with the geometric constructions of planar transformations to illustrate some of the difficulties translating the functionality of this simple toolkit into code. We will introduce vectors and show how this can help us represent a large class of transformations. |
| Agenda |
|
| Uses Tool(s) | |
Constructing Planar Transformations with Compass/Straightedge
Take a look at the implementations for "Mirror" and "Move" on the compass-straightedge constructions page.
Let's focus on where we had to use something more than just the four functions AddLine (straightedge), AddCircle (compass), findIntersection, and dist.
For "Mirror", we almost got away with using only the four functions, but we had to check first that the given point was not on the line segment (findIntersection isn't general enough to find any intersection -- only ones between two curves). It's hard to replace what the eye can do so easily with the eye in code. Using the function LineClosestPoint, we can find the closest point to P on l. For P within the "typical" range, this will give us perpendicular projection of P onto l. Notice that theoretically, the closest point to a line of a point on the line should be the point itself, so it is tempting to say
if dist(closest, pIn) >0:
but it is prudent to assume that nothing evaluates to exactly 0 in a computational sense. In our case, we choose a tolerance relative to the unit scale of the canvas.
For "Move", our relatively clean algorithm was compromised by our having to access coordinates of the points to check which of the intersection points was the correct one. This once again highlights that while it is easy to translate the basic functionality of compass and straightedge to code, that it is more difficult to translate what one can easily do with the eye (detecting intersections, checking to see whether two lines are close to parallel). To help us with this, we will introduce vectors.
Vectors - Representation and Manipulation
How do vectors relate to points?
This question really only makes sense when we are looking at vectors in the familiar vector spaces <math>\R^{2}</math> and <math>\R^{3}</math> where we are used to defining a point as an ordered set of numbers. In this case, we can simply identify the head of a vector with a point. Try to get used to thinking of manipulating vectors in diagram, rather than manipulating the coordinates of the points.
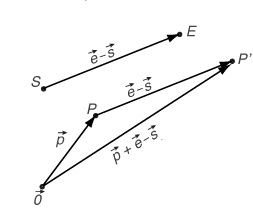
Returning now to the "Move" transformation, this picture tells us how P' relates to P, S (startpoint) and E (endpoint).
Using the vector capabilities in the rhinoscript package, this can be easily translated:
def Move(startPoint, endPoint, pIn): return rs.VectorAdd(pIn,rs.VectorSubtract(endPoint,startPoint))
Vectors: Length, Distance, and Dot Product
Check out the Length, Distance and Dot Product page.
Projecting a Point on a Line
We took the example of the transformation "Mirror" to show some of the difficulties that arise in trying to reflect a point across an axis (an infinite line). We are tempted to use a slightly altered version of MakePerpendicular Line, using the function LineClosestPoint.
def MirrorTake1(lineIn, pIn): closest = rs.LineClosestPoint(lineIn, pIn) return rs.VectorAdd(closest, rs.VectorSubtract(closest, pIn))
The problem here is that LineClosestPoint literally returns the closest point on the line segment to pIn, so if you supplied a point whose perpendicular line does not intersect with the line segment, you will get something different than the projected point onto the line (as understood as an infinite line). With the help of vectors -- in particular the important operation of dot product -- we can write a function called LineProjectedPoint which returns the closest project point treating the line as an infinite line.
def LineProjectedPoint(lineIn, pIn): pLine0 = lineIn[0] pLine1 = lineIn[1] u = rs.VectorUnitize(rs.VectorSubtract(pLine1, pLine0)) projectedScale = rs.VectorDotProduct(rs.VectorSubtract(pIn, pLine0), u) return rs.VectorAdd(pLine0, rs.VectorScale(u, projectedScale)) rs.AddPoint(LineProjectedPoint(line, pOff)) #now we can write a Mirror function that does what we want def Mirror(lineIn, pIn): projected = LineProjectedPoint(lineIn, pIn) if dist(projected, pIn) > rs.UnitAbsoluteTolerance(10**(-5), True): return rs.VectorAdd(projected, rs.VectorSubtract(projected, pIn)) else: return pIn
Transformations
The transformations page details examples of specific classes of transformations such as plane transformations and linear transformations
Transforming using matrices
As we've seen, many transformations can be represented by matrices. The rhinoscript package makes it easy to express some of the most often used transformations in terms of matrices. In fact, all you need to do is to feed in the input and the output is given as a matrix. Here are the implementations of the plane transformations that we have been working with, in terms of matrices (Xforms):
def MoveX(startPoint, endPoint, pIn): matrix = rs.XformTranslation(rs.VectorSubtract(endPoint, startPoint)) return rs.PointTransform(pIn, matrix) def MirrorX(lineIn, pIn): pLine0 = lineIn[0] pLine1 = lineIn[1] normal = rs.VectorUnitize(rs.VectorCrossProduct([0,0,1], rs.VectorSubtract(pLine1, pLine0))) matrix = rs.XformMirror(pLine1, normal) return rs.PointTransform(pIn, matrix) def RotateX(centerPoint, angle, pIn): matrix = rs.XformRotation2(angle, [0,0,1], centerPoint) return rs.PointTransform(pIn, matrix) def ScaleX(startPoint, factor, pIn): matrix = rs.XformScale(factor, startPoint) return rs.PointTransform(pIn, matrix)
Assignment
You will be using plane transformations to create a pattern of line segments filling out a canvas of fixed dimension 110 units (tall) x 170 units (wide) in the plane.
You might start with a transformation (like any of the ones introduced in class eg. "Move", "Mirror", "Scale", "Rotate", any matrix transformation, or combinations of any of these) and repeatedly applying it to an initial line segment. Or you might proceed more systematically by drawing fixed length line segments along a grid and then transforming each one in a way that depends on its position in the plane, such as in the example below.
Give some thought to your composition. A good composition should have an element of play but always of control. You should have some natural stopping condition, such as the boundaries of your canvas, or some other criteria such as nonoverlapping segments.
Place your code as well as an image of your composition into the Dropbox folder before class.